0. Abstract
- 생략
1. Introduction
- CNNs가 점점 deep해지면서, input 혹은 gradient passes 가 많은 layers 지나면서, 이것이 vanish되거나 "wash out"되는 새로운 research problem 부상하였다.
- 최근에 많은 논문들이 이러한 문제를 다루고 있다. 예를 들어 ResNets와 Highway Networks의 경우 one-layer에서 다음 layer로 독립적인 connection을 통해 신호를 by-pass(우회)하거나, FactalNets은 반복적으로 평행한 layer sequence를 결합한다.
- 이러한 다른 방법들은 모두 하나의 key characteristic을 공유하고 있는데, 바로 early layers과 later layers 사이의 short path를 만들어 준다는 점이다.
- 본 논문에서는, 이러한 insight의 정수(distill)를 빼 내어 하나의 간단한 연결 패턴을 만들어 낸다. 모든 layer를 연결(feature-map size를 맞춰주면서)함으로써, 이를통해 네트워크 안의 layers 사이에 최대한의 정보를 보장해 준다.
- feed-forward nature를 보존하기 위해, 각각의 layer은 모든 선행 레이어로부터 추가 입력을 얻고 자체 feature map을 전달한다. (Fig.1 참조)
- 여기서 중요한 점은, DenseNet은 ResNet과 달리 features를 summation을 통해 combine하지 않고, concatenating을 통해 features를 combine한다는 점이다. 그런 이유로, l번째 layer은 모든 선행 convolution block의 featuremap으로 구성된 입력을 가진다.
- 이와 같은 성질 때문에, L-layer network에는 기존의 전통적인 architecture의 connection의 갯수인 L개가 아니라, ㅣ(ㅣ+1)/2 개의 connection을 가진다.
- 이러한 dense connectivity pattern 때문에, 본 논문에서는 이런 접근 방법을 Dense Convolutional Network(DenseNet)이라고 부른다.
-Dense하게 connect되었다는 생각에서 오는 직관과 반대로, 이러한 dense-connectivity pattern은 더 적은 parameters를 요구하는데, 왜냐면 이러한 방법은 중복되는 feature-maps를 다시 배울 필요가 없기 때문이다.
- 최근의 ResNets의 변형들은 많은 layers이 training동안 매우 적게 contribute하고 그리고 사실 random하게 dropped될 수 있다는 것을 보여주고 있다. 이는 recurrent neural networks와 비슷한데, 이러한 방법을 통해서도 각각의 layer에는 이것의 고유의 weights를 가지고 있기 때문에 상당히 많은 parameter가 필요로 하였다.
-본 논문의 DenseNet은 명시적으로 network에 더해질 정보와 보존될 정보를 차이를 두고 있다.
-DenseNEt layers는 매우 narrow하고(예를 들어, 한 layer당 12개의 filter가 존재), 네트워크의 "collective knowledge"에 적은 수의 feature-maps만 추가하고 나머지 featuremaps은 변경하지 않는다. 그리고 마지막 classifier는 모든 feature-maps를 기반으로 의사 결정을 한다.
- parameter의 efficiency뿐만 아니라, DenseNEt의 하나의 큰 advantage는 information과 gradient의 vanishing problem을 해결했다는 점이다. 각각의 layer은 loss function과 original input signal로부터 직접적으로 gradients를 접근할 수 있어서, 암묵적으로 심층 감독(deep supervision)이 가능하게 된다.
- 또한, dense connections은 regularizing effect가 존재해서, smaller training set sizes로도 overfitting을 감소시킬 수 있었다.

2. Related Work
- 생략
3.DenseNets
- x0 : single image that is passed through a convolutional network
- L : the number of network's layers , each of which implements a non-linear transformation H(l)(.), where l indexes the layer.
- H(l)(.) : composite function of operations such as Batch Normalizationm ReLU,Pooling, or Convolution
- x(l) : the output of the lth layer
* ResNets Vs Dense connectivity
1) ResNEts

- 장점 : gradient가 identitiy function을 통해 directly하게 들어갈 수 있다. 그러나, identitiy function과 H(l)의 output은 summation을 통해 combine되기 때문에, network의 imformation의 흐름을 방해한다.
2)Dense connectivity
- layers 사이의 information flow를 더욱 증가하기 위해, 본 논문은 다른 connectiviy pattern인, 모든 layer에서 모든 후속 layer으로 직접 연결을 제안한다. (Fig1 참조)
- 결과적으로, l번째 layer 모든 전례하는 layers를 받게 되고, 그것을 input으로 이용한다.

* [x0,.....,xl-1] : concatenation of the feature maps produced in layers 0 ,...,l-1
* Composite function
- 본 논문에서는 H(l)(.)을 3개의 연속적인 operation으로 정의한다 : batch normalization(BN), ReLU, 3*3 convolution
* Pooling layers
- feature map의 크기가 변경되면, Eq.(2)에 사용된 연결 연산은 사용할 수 없다. 그러나 convolution network의 필수적인 부분은 feature map의 size를 변경하는 downsampling layer이다.( 즉, 우리는 downsampling layer로 featuremap의 size를 동일하게 바꿀 수 있다.) architecture에서 downsampling을 용이하게 하기 위해, network를 densely connect된 여러 개의 dense block으로 분할한다. (Fig2 참조)
- 본 논문은 block 사이의 layer를 convolution과 pooling을 하는 transition layer 라고 부르고, 실험에 사용된 transition layer은 batch normalization layer과 1*1 convolution layer, 그리고 그 뒤에 2*2 average pooling layer로 구성된다.

* Growth rate
- Dense Block 내의 레이어는 k개의 feature map을 생성한다. 그리고 이 k는 Growth rate라고 부르는 hyperparameter이다. 본 논문에는 k=12를 사용한다. l번째 layer에는 k0 + k*(l-1)개의 입력값(channel 수라고 생각하면 됨)을 갖는다. k0은 입력 layer의 channel 수 이다. 본 논문에서는 이 값이 작아도 된다고 한다!
- 예를 들어, 한 Dense Block안에서의 각각의 layer는 앞에 있는 feature-maps를 접근해야 하고, 그러므로, network의 "collective knowledge"에 접근한다는 것이다. 각각의 layer은 현재 state에 자체 feature-maps k를 더한다
- 이 growth rate를 통해 각각의 layer가 전체 state에 기여를 하는 정도를 제한한다.
* Bottleneck layers
- 기존에 제안된 bottleneck layer를 이용하면, 특별히 denseNet에 더욱 효과적이기 때문에, 이러한 구조를 이용한다고 한다. 즉 , H(l)(.)에 Bottleneck을 적용한다. (i.e., BN-ReLU-Conv(1*1)-BN-ReLU-Conv(3*3))
-본 논문에서는, 각각의 1*1 convolution을 통 input feature map의 channel개수를 줄이고, 다시 입력 feature map의 channel 개수 만큼을 생성하는 대신 growth rate 만큼의 feature map을 생성하는 것이 차이고, 이를 통해 computational cost를 줄일 수 있다고 한다.
* BottleNeck이란?
- Channel 값이 많아지는 경우 연산에 걸리는 속도도 그 만큼 증가할 수 밖에 없는데, 이 때 Channel의 차원을 축소하는 개념.
* Compression
- 모델의 compactness를 위해, 본 논문에서는 transition layers에서 feature-maps의 수를 줄일 수 있었다.
- 만약 dense block이 m개의 feature-maps를 가지고 있다면, 본 논문에서는 그 이후로 오는 transitional layer를
[θm]의 output feature-maps를 생성하도록 두었다.
* 0<θ<1 : referred to as the compression factor
- when θ = 1, the number of feature-maps across transition layers remains unchanged
- 본 논문에서는 θ<1을 DenseNet-C라고 언급하고, θ = 0.5 값으로 실험을 진행하였다.
- 만약 bottleneck 및 transition layer에서 θ<1인 경우를 모두 사용할 경우, DenseNEt-BC로 부른다.

* Implementation Details
- ImageNet의 경우를 제외하고는, DenseNet은 3개의 dense blocks-각각의 block이 layer 수가 같은-로 이루어져 있다.
- 첫 denseblock에 들어가기 전에, output channels의 수가 16인 convolution이 input image에 일어난다.
- 3*3 convolution kernel에서는, 각각의 input에 one-pixel만큼 zero-padded된다.
- transition layer에서는 1*1convolution과 그 이후 2*2 average pooling을 이용하였다.
- last dense block에서는, global average pooling이 수행되고 그리고 softmax classifier가 적용된다.
- 각각 3개의 dense block의 feature-map은 32*32, 16*16, 그리고 8*8이다.

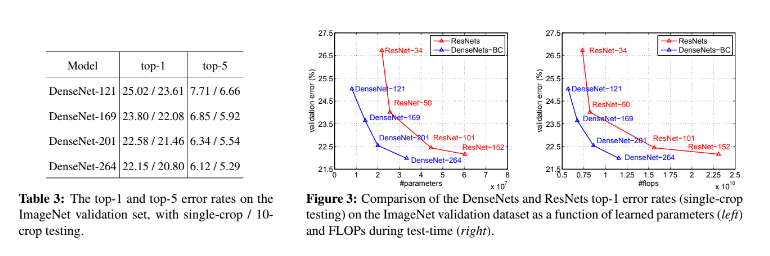
4.Experiments